3 Folgen und Reihen

3.5 Reihen

Nachdem wir die Grenzwerte von Zahlenfolgen studiert haben, können wir unser neu erworbenes Wissen sogleich auf häufiger in der Physik vorkommende Dinge anwenden, wie etwa unendliche Summen , die Reihen genannt werden:

Diese werden schon hin und wieder bei interessanteren physikalischen Fragestellungen gebraucht: Wenn wir z.B. die elektrostatische Energie einer Kette von unendlich vielen äquidistanten abwechselnd positiven und negativen Punktladungen für ein Kettenglied aufsummieren wollen (die ein einfaches, aber erstaunlich gutes eindimensionales Modell für einen Ionenkristall darstellt) stoßen wir auf die unendliche Summe über die Glieder der alternierenden harmonischen Folge (F7): die Reihe . Wie rechnet man das aus ?

Reihen sind Folgen, deren Glieder endliche Summen reeller Zahlen sind: Die Definition der

führt die Reihen auf die Folgen zurück, die wir oben gerade behandelt haben.

Insbesondere ist eine Reihe genau dann konvergent und hat den Wert , wenn die Folge ihrer Teilsummen (nicht etwa die ihrer Summanden !!) konvergiert: :

Auch das Vielfache einer konvergenten Reihe und die Summe und Differenz von zwei konvergenten Reihen sind wieder konvergent.

Die wenigen Musterbeispiele für Reihen, die nötig sind, um das Wichtigste bereits sehen zu können, gewinnen wir am einfachsten durch stückweises Aufsummieren unserer Musterfolgen:

Die Reihe (R1) aus den Teilsummen der Folge (F1) der natürlichen Zahlen: ist klarerweise divergent.

Die Reihe (R2) aus den Gliedern der alternierenden Folge (F2) hüpft immer zwischen und hin und her, hat demnach zwei Häufungspunkte, also keinen Grenzwert.

Auch die aus den Gliedern der harmonischen Folge (F3) aufsummierte "harmonische Reihe" (R3), d.h. die Folge ist divergent. Denn das (auch notwendige) Cauchy-Kriterium ist nicht erfüllt:
Wenn wir z.B. wählen und für ein aus Gliedern bestehendes Stück der Reihe betrachten:
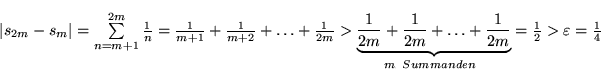, während zur Konvergenz doch erforderlich gewesen wäre.

Deren alternierende Variante (R7), gebildet aus der Folge (F7), unser physikalisches Beispiel von oben konvergiert jedoch ( , wie wir später zeigen werden). Wegen dieses Unterschieds zwischen Reihen mit positiven Gliedern und alternierenden ist es zweckmäßig, einen neuen Begriff einzuführen: Eine Reihe heißt absolut konvergent, wenn bereits die Reihe der Beträge konvergiert.

Man kann leicht verstehen, dass bei einer absolut konvergenten Reihe die Summanden ohne Schaden für den Grenzwert umgeordnet werden können. Zwei absolut konvergente Reihen können gliedweise zu einer neuen absolut konvergenten Reihe multipliziert werden.

Für die absolute Konvergenz haben die Mathematiker verschiedene hinreichende Kriterien, die sogenannten Majoranten-Kriterien entwickelt, mit denen Sie sich in der Vorlesung über Analysis noch ausführlich beschäftigen werden:

Als Majoranten dienen dabei sehr häufig die "geometrischen Reihen" (R6): , die aus den geometrischen Folgen (F6) hervorgehen. Bei deren Berechnung kommt uns die früher für hergeleitete geometrischer Summe zugute:

d.h. konvergent für und divergent für .

Die Reihe der inversen natürlichen Fakultäten (R4) wollen wir genauer betrachten:

Wir sehen zunächst, dass die Folge der Teilsummen monoton steigt: .

Zur Berechnung der oberen Schranke schätzen wir durch die majorante geometrische Summe mit ab:

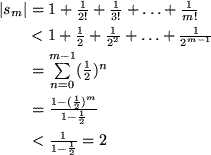
Da die monoton steigende Folge der Teilsummen also durch nach oben beschränkt ist, garantiert uns der Satz von Bolzano und Weierstraß die Konvergenz. Nur den Grenzwert kennen wir noch nicht. Dieser Grenzwert ist nun tatsächlich etwas völlig Neues, eine irrationale Zahl. Wir nennen sie , so dass die Zahl nach der ergänzenden Konvention folgendermaßen durch die mit beginnende Reihe definiert wird:

Zur Bestimmung des numerischen Wertes von rechnen wir uns die Glieder der Nullfolge (F4) einmal aus:

und summieren die Teilsummen:

Wenn wir die rasche Konvergenz betrachten, können wir uns leicht vorstellen, dass man nach kurzer Rechnung für den Grenzwert

erhält.

Damit haben wir einen ersten Überblick über die Grenzprozesse gewonnen und einige für die Naturwissenschaften wichtige Folgen und Reihen mit ihren Grenzwerten kennengelernt, die uns im folgenden helfen werden.