(Tylko strona po angielsku jest cała oraz często aktualizowana)
Rozprawę doktorską obroniłem w Instytucie Matematyki i Informatyki
Uniwersytetu Münster w Westfalii (w Niemczech). Tam miałem to szczęście, że jeden z
ekspertów w kwantowej teorii pola (w szczególności w aspektach
konstruktywnych à la Osterwalder-Schrader), Prof. dr. hab. Raimar Wulkenhaar,
był moim
promotorem. Tematem pracy były równania Schwingera-Dysona (równania pętlowe) oraz
tożsamość Warda-Takahashiego dla tensorów losowych (zob. poniżej).
Od 2019 do 2021 roku pracowałem w Warszawie (Wydział Fizyki Uniwersytetu
Warszawskiego) w fantastycznej grupie Prof. dr. hab. Piotra Sułkowskiego.
Od września 2021 roku pracuję, jako adiunkt naukowy, w Heidelbergu (Instytut
Fizyki Teoretycznej) w grupie Prof. dr. hab. Răzvana Gurău.
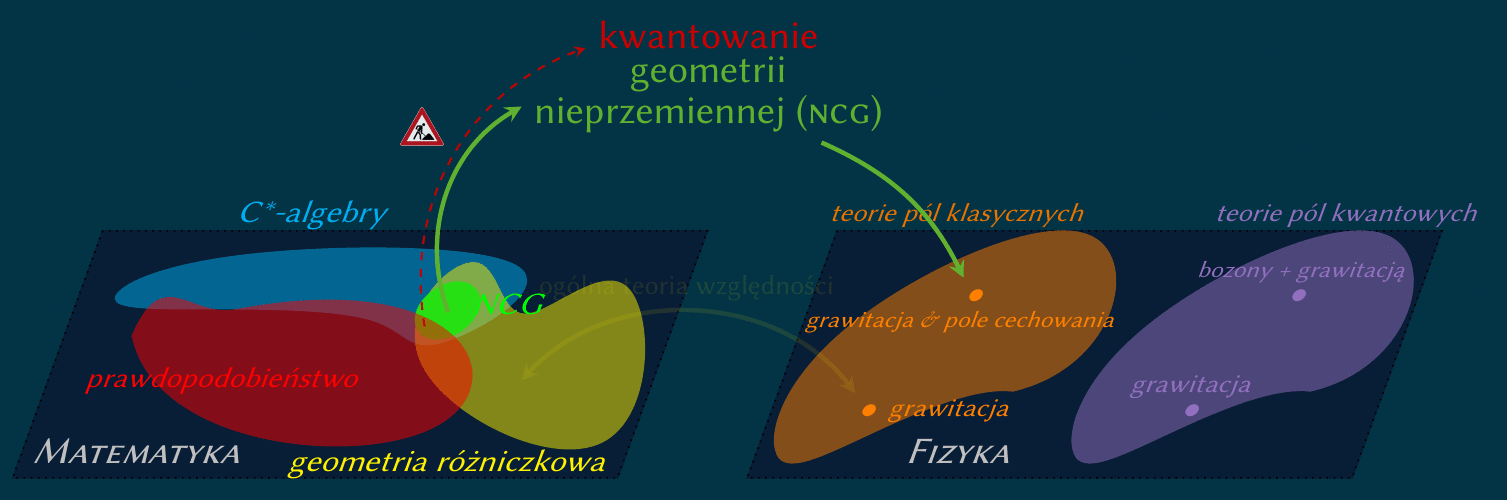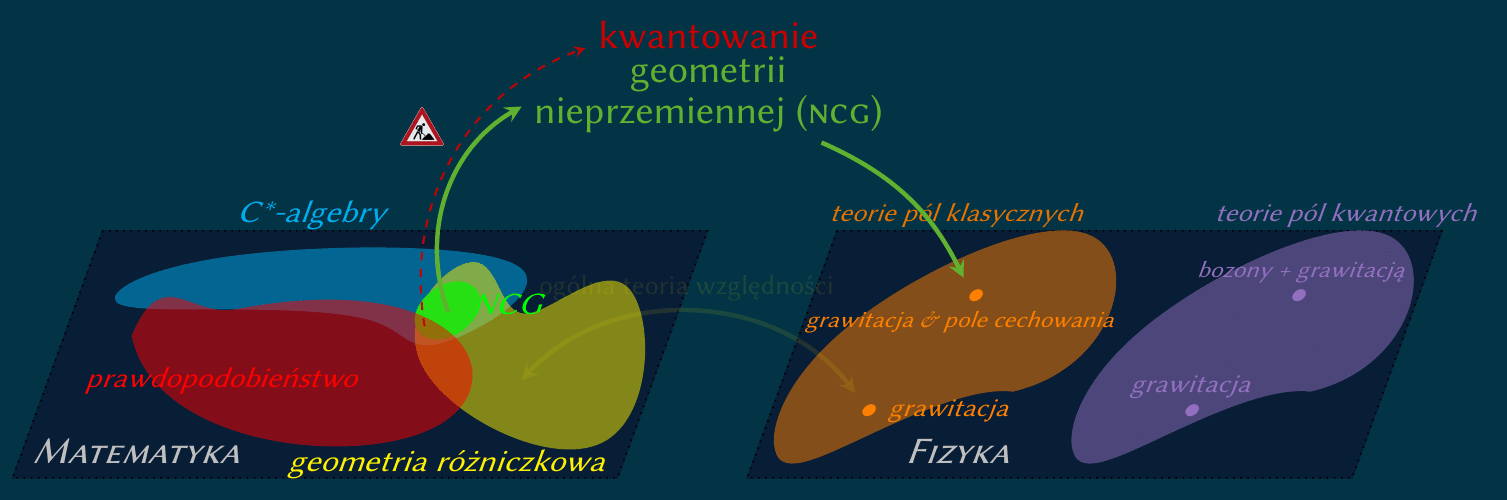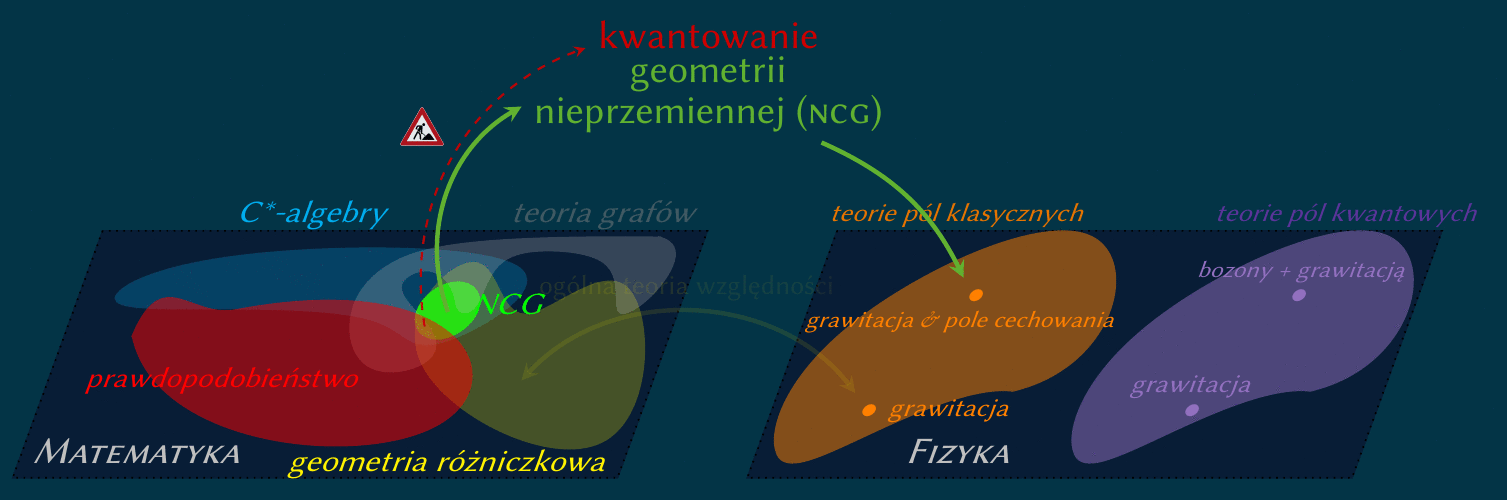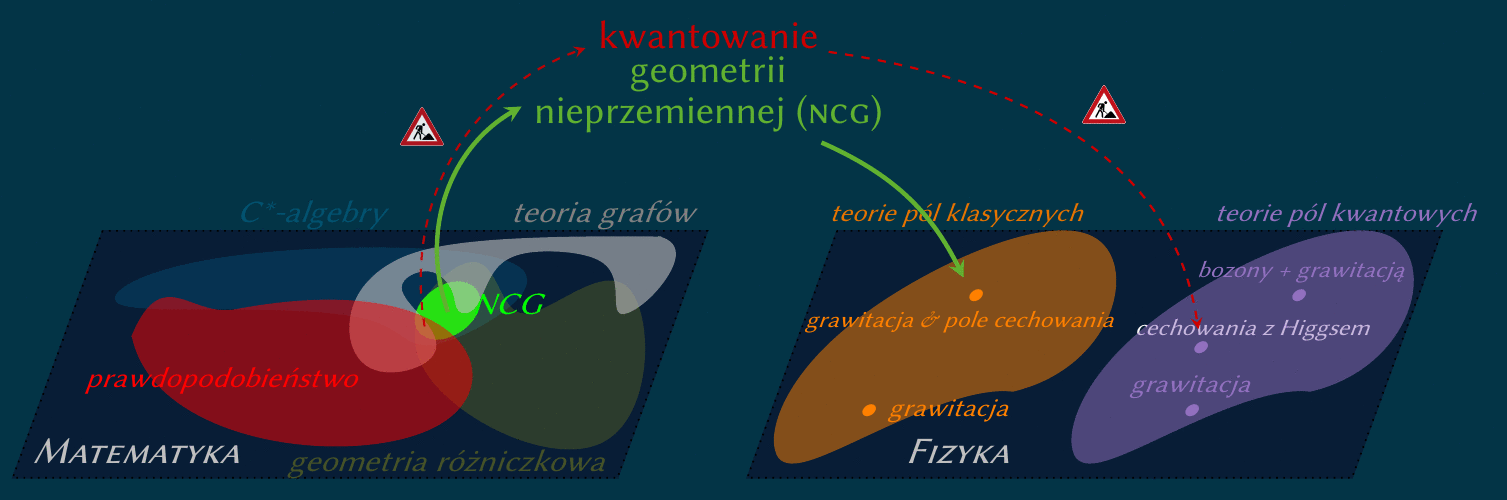
Interesuję się grawitacją kwantową, szczególnie z punktu widzenia geometrii losowej,
którą można rozumieć jako euklidesową kwantową teorię geometrii.
Zdefiniowanie sumy statystycznej na gładkich czasoprzestrzeniach (rozmaitościach
różniczkowalnych) opisujących klasyczną teorię grawitacji nie jest często możliwe.
Dlatego też przybliżenia dyskretne
mogą być użyteczne. Pomocnym jest np. przybliżenie symplicjalne („PL-manifolds”). Tensory losowe (R. Gurău) generują właśnie tego typu kompleksy,
których krzywiznę można liczyć stosując formalizm Regge'a(-Einsteina-Hilberta).
Podczas mojego pobytu w Warszawie zajmowałem się
opisem dualnym. Jest to formalizm spektralny Connesa-Chamseddine'a,
bazujący na postulacie, że działanie klasyczne jest śladem funkcji tylko
operatora Diraca.
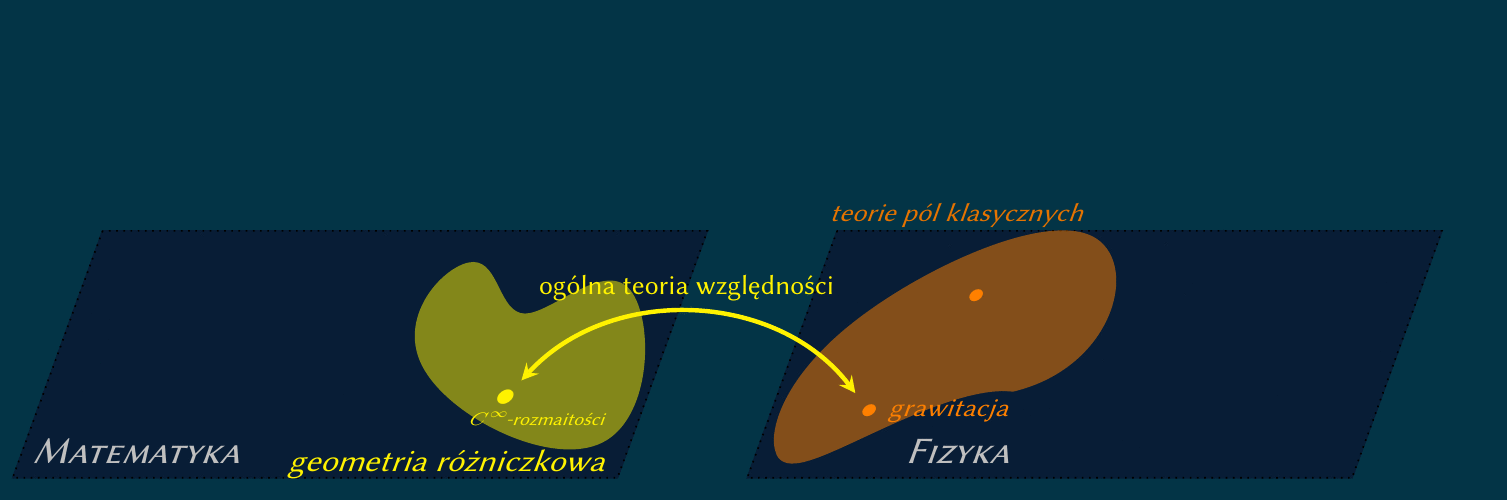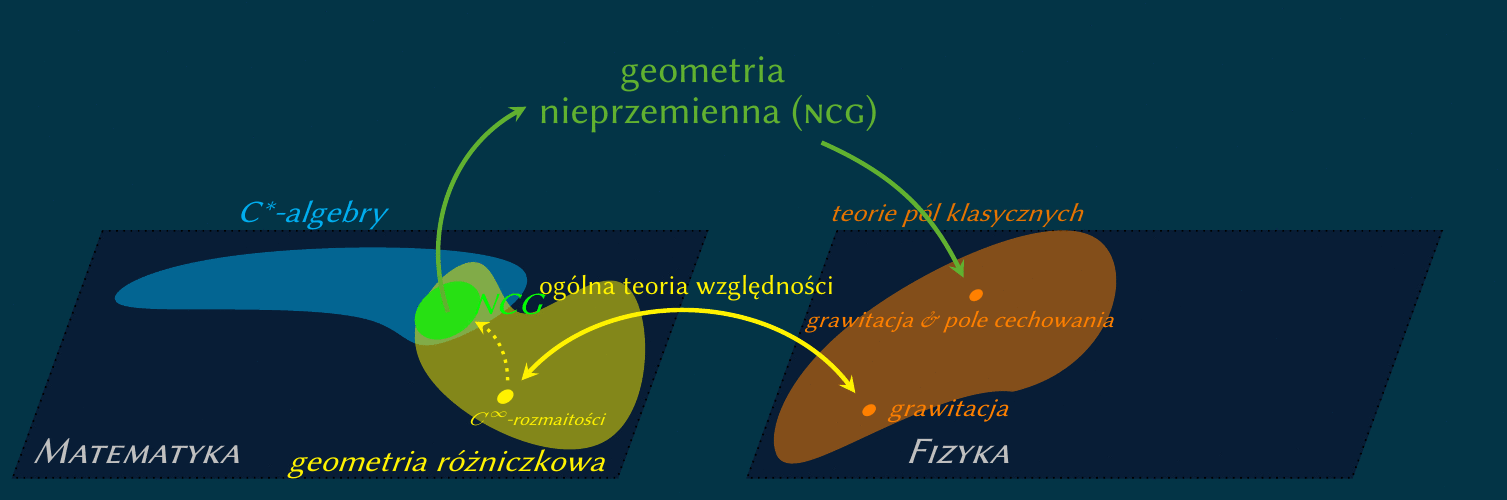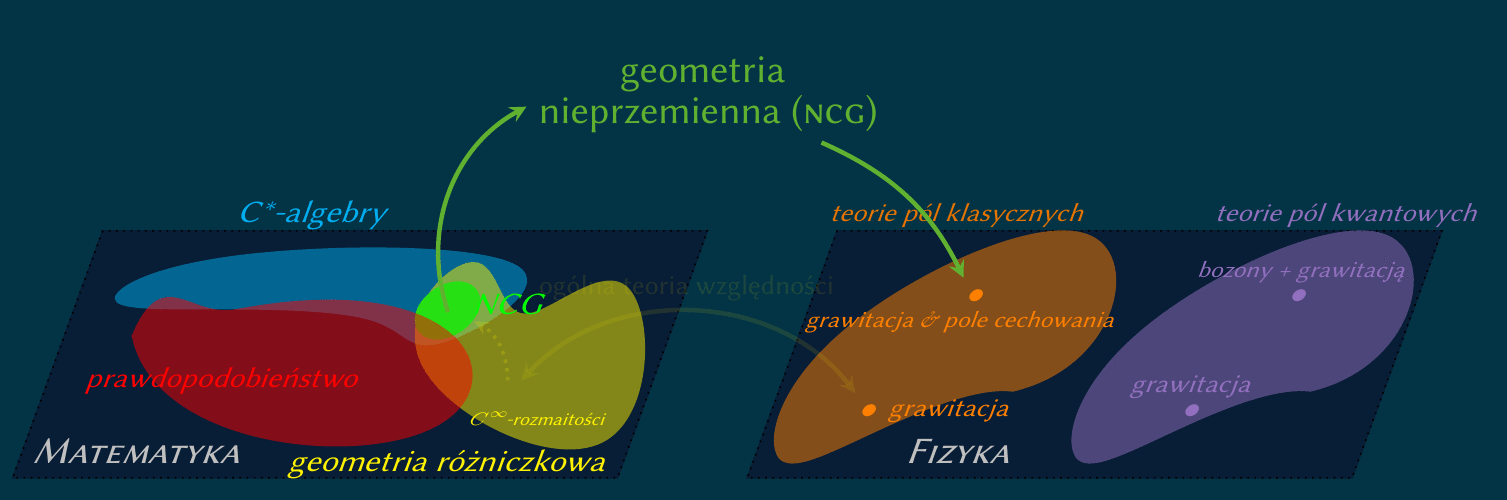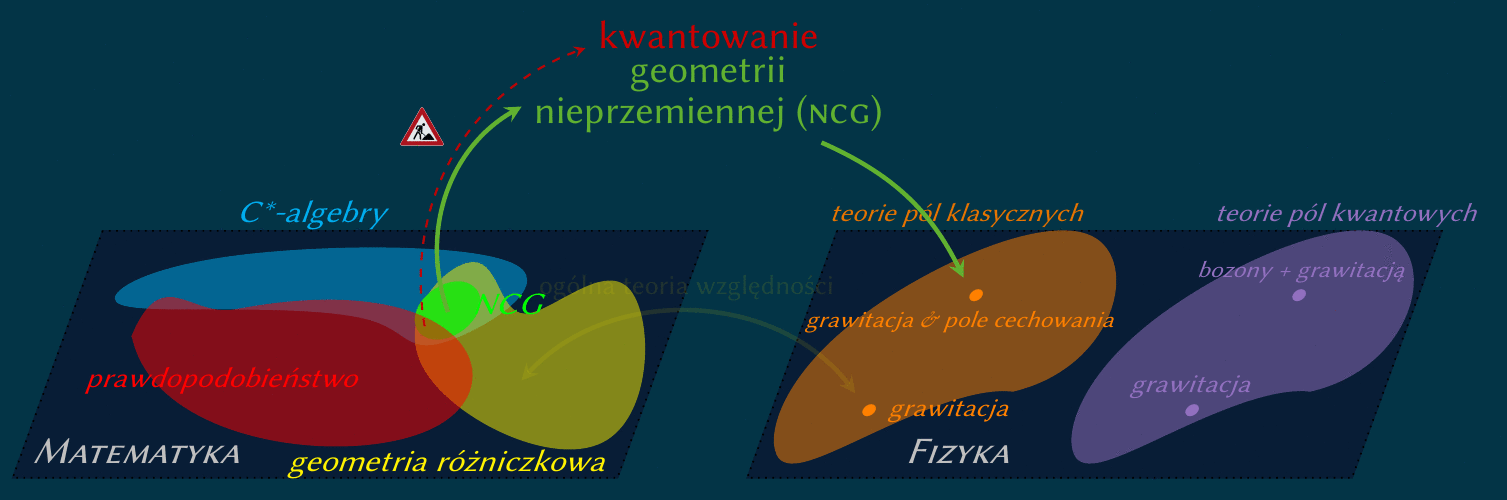
Niestety problem z definicją całki po trajektoriach nadal występuje w tym sformułowaniu.
Jednakże przybliżenie macierzowe, znane jako geometria rozmyta (ang. fuzzy) albo macierzowa
reguluje sumę statystyczną na szczęście do takiej postaci, że problem redukuje się bardzo dobrze znanego w matematyce--teorii macierzy przypadkowych.
Związek tego typu przybliżeń
skończeniewymiarowych z macierzami losowymi jest bardzo typowy dla wielu zagadnień
matematyki, fizyki i ogólnie tych występujących w naturze. Również dla tensorów
przypadkowych modele macierzowe nadal pozostają źródłem inspiracji.
Kiedy kandydat na teorię kwantowej grawitacji jest już sformułowany, potrzebne jest narzędzie, które
umożliwia interpolację pomiędzy wysokimi (UV) a niskimi (IR) energiami. W tym kontekście ostatnio
interesuję się też aspektami matematycznymi funkcjonalnej grupy renormalizacji (równanie Wettericha) .
Jestem zainteresowany współpracą w ramach „4EU+ European University
Alliance”, Kopenhaga-Heidelberg-Mediolan-Paris(Sorbonne)-Praga-Warszawa (ale też niekoniecznie tylko w ramach tego programu).
Dziękuję panu Arkadiuszowi Bochniakowi za poprawienie
kilka błędów gramatycznych w pierwszych wersjach tutejszej strony.
Cieszę się na Twoją wiadomość:
Impressum:
Carlos I. Perez-Sanchez
Instytut Fizyki Teoretycznej Uniwersytetu Ruperto Carola w Heidelbergu,
Philosophenweg 19, 69120, Heidelberg, Niemiec.
I don't read Polish, send me back to English home page
Angielski 
Francuski 
Hiszpański
Niemiecki