Je m'intéresse à la gravité quantique, notamment du point de vue de la géométrie aléatoire, qui peut être conçu comme la théorie quantique euclidienne de la géométrie.



Depuis l'automne de 2021, je travaille à l'Université Heidelberg (Institut de Physique Théorique) dans le groupe du Prof. Razvan Gurau. Avant, de 2019 à 2021, j'ai travaillé en Pologne (Département de Physique Theoretique, Université de Varsovie) dans le groupe fantastique du Prof. Piotr Sułkowski.

Auparavant, j'ai soutenu ma thèse à l'Institut de Mathématiques de l'Université de Münster en Westphalie (Allemagne). Là, j'ai eu la chance que l'un des experts de la théorie quantique des champs (en particulier les aspects constructifs et axiomatiques à l'Osterwalder-Schrader), Prof. Wulkenhaar, été mon directeur de thèse. Celle-ci porte sur les équations de Schwinger-Dyson, aussi connu comme la méthode des équations de boucles, et l'identité Ward pour les tenseurs aléatoires (voir ci-dessous).

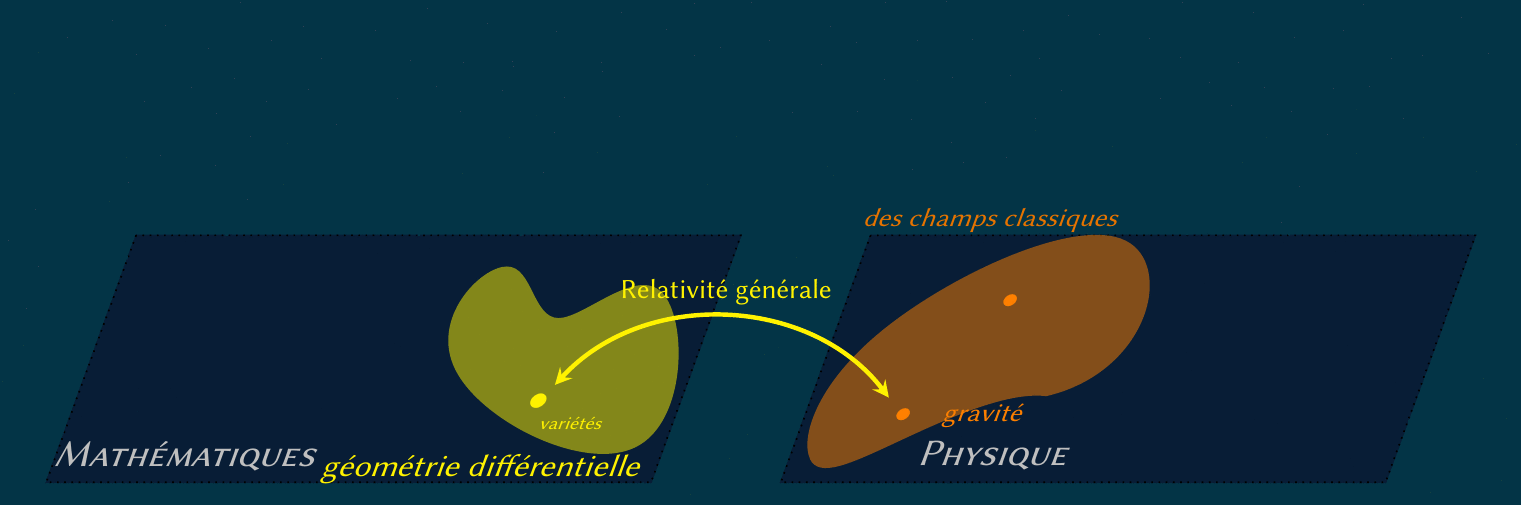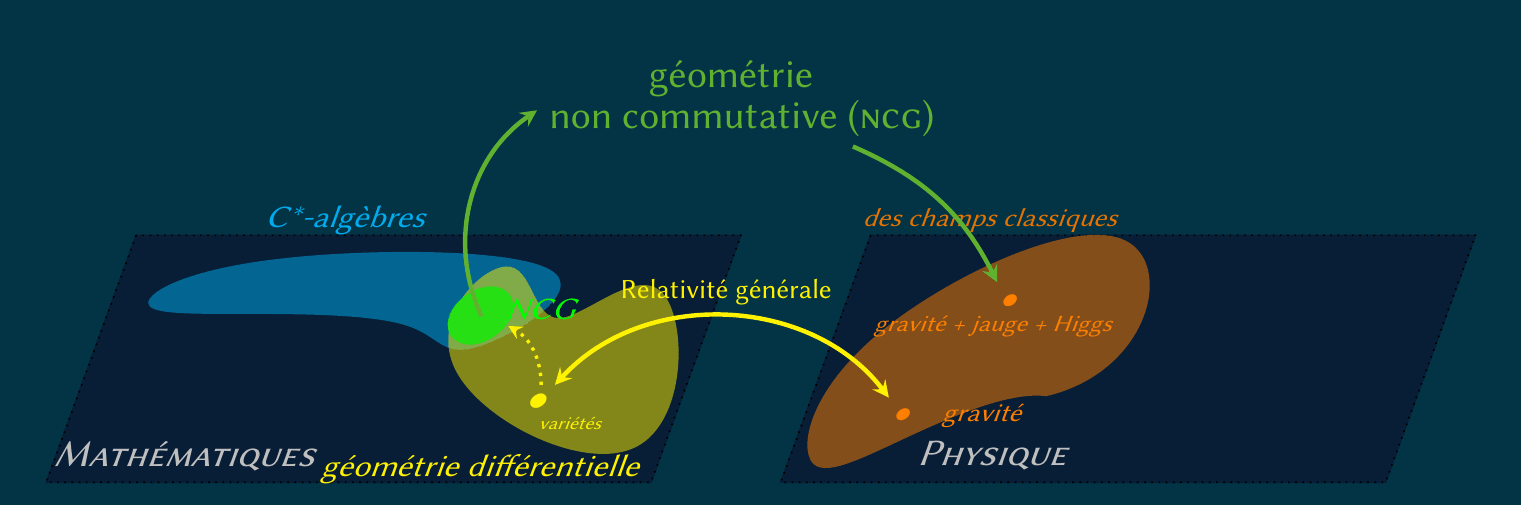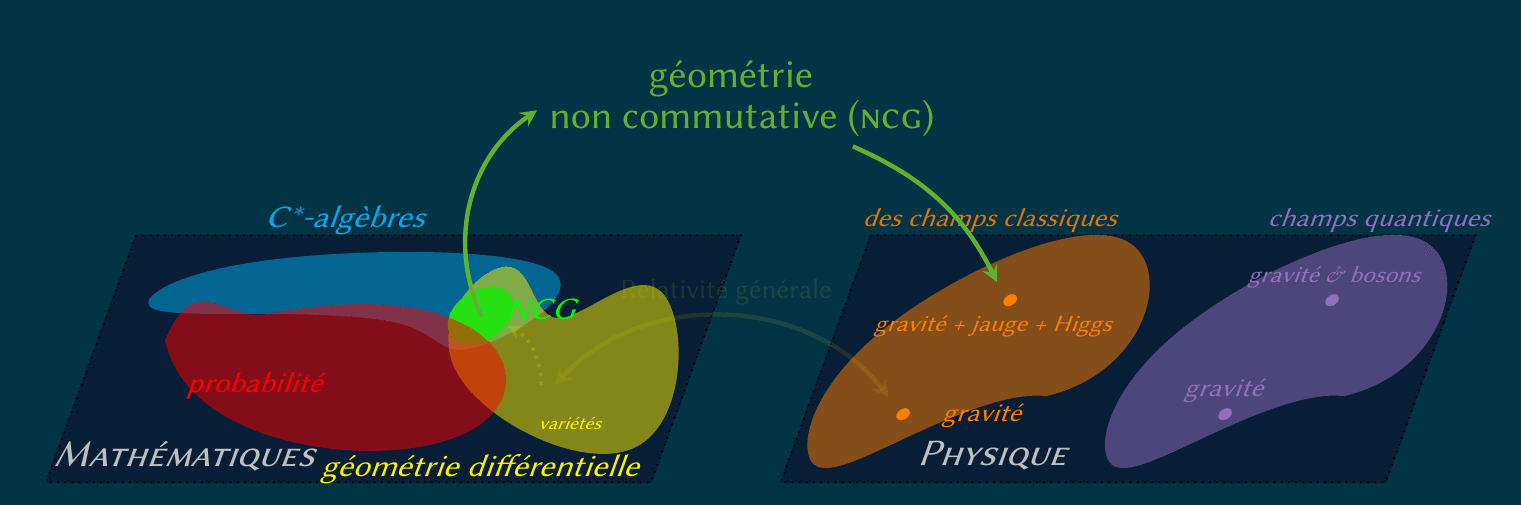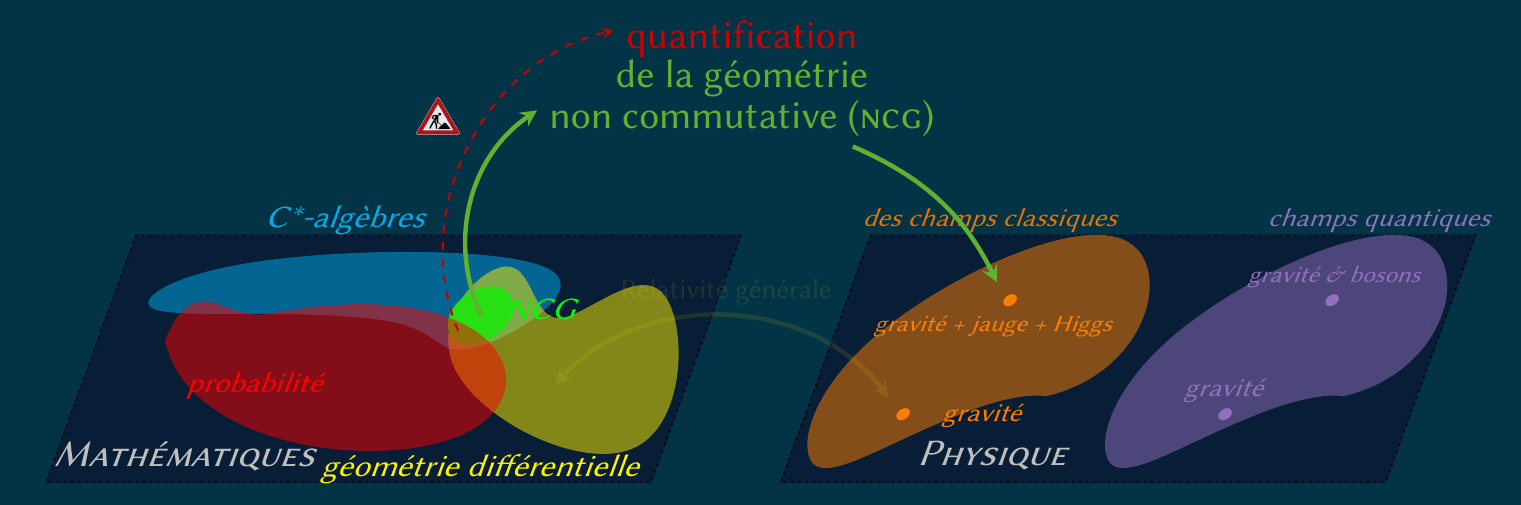
Pendant mon séjour à Heidelberg et Varsovie, j'ai traité le formalisme spectral de Connes-Chamseddine, basé sur le postulat que l'action classique peut dependre uniquement du spectre de l'opérateur de Dirac (elle est donc une trace de certain fonction de cet operateur). Le problème de n'avoir pas définition (acceptée par toute la communauté) de l'intégrale de chemin persiste encore dans cette formulation. Cependant, l'approximation matricielle, connue sous le nom de géométrie floue (ang. fuzzy) ou matricielle, régule heureusement la fonction de partition sous une forme telle que le problème se réduit à la théorie des matrices aléatoires, très connue en mathématiques. La relation entre de telles approximations à dimension finie et des matrices aléatoires est très typique de nombreux problèmes en mathématiques, en physique (généralement de ceux qui se produisent dans la Nature). Pour les tenseurs aléatoires également, les modèles matriciels restent une source d'inspiration.



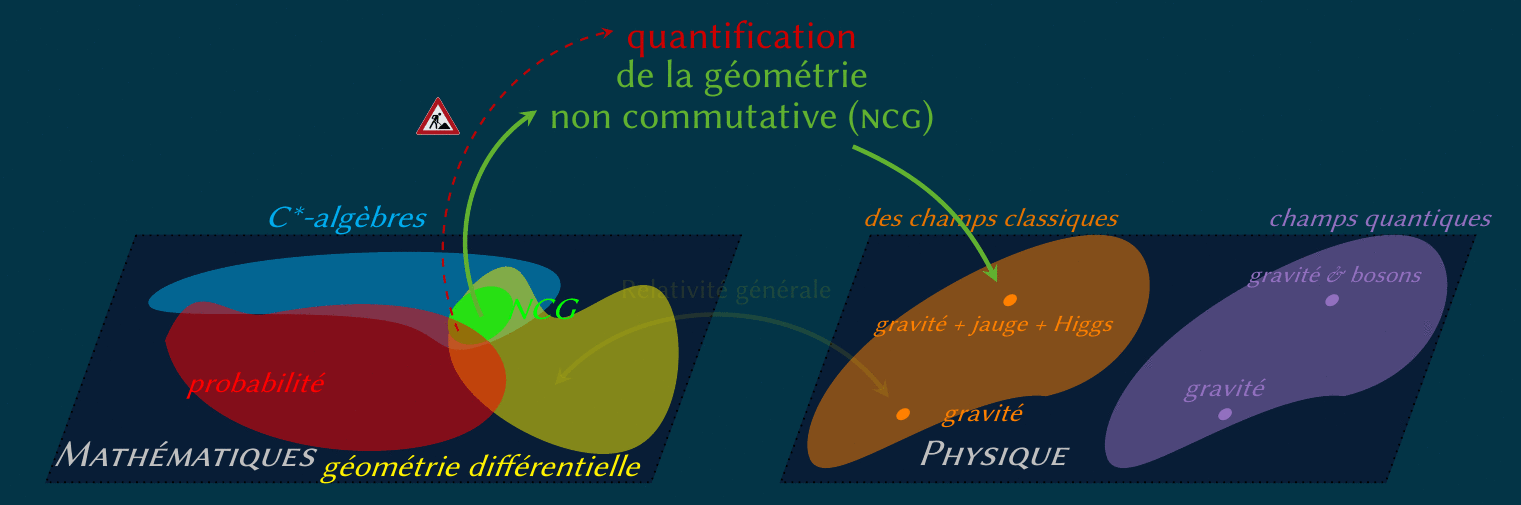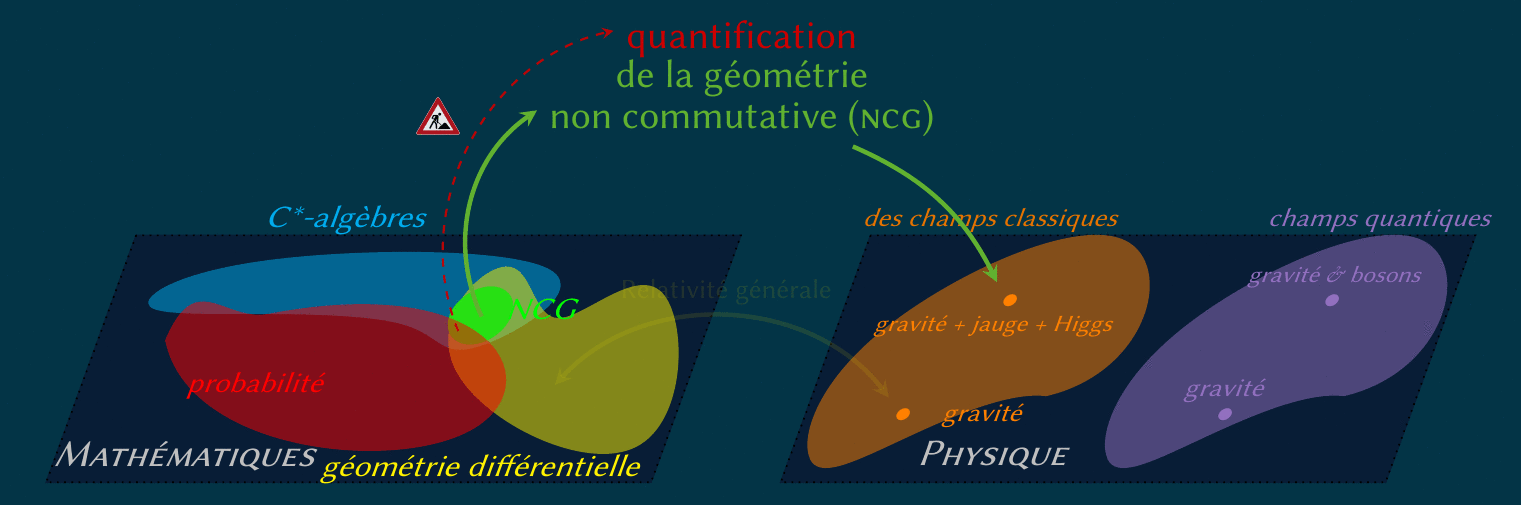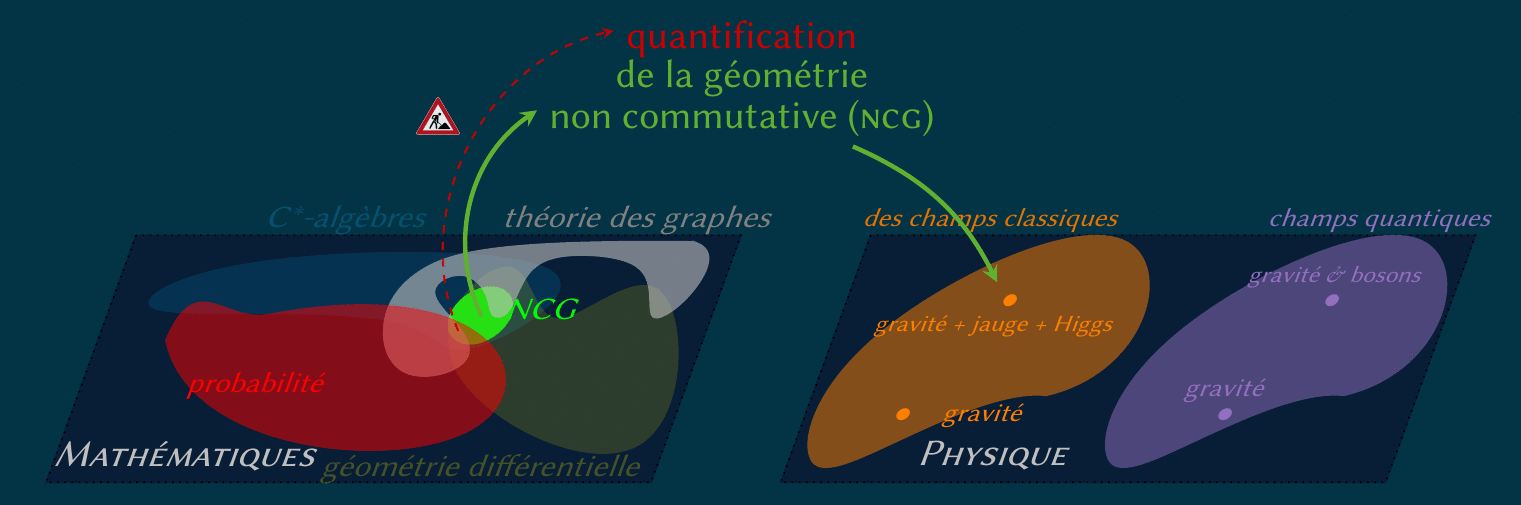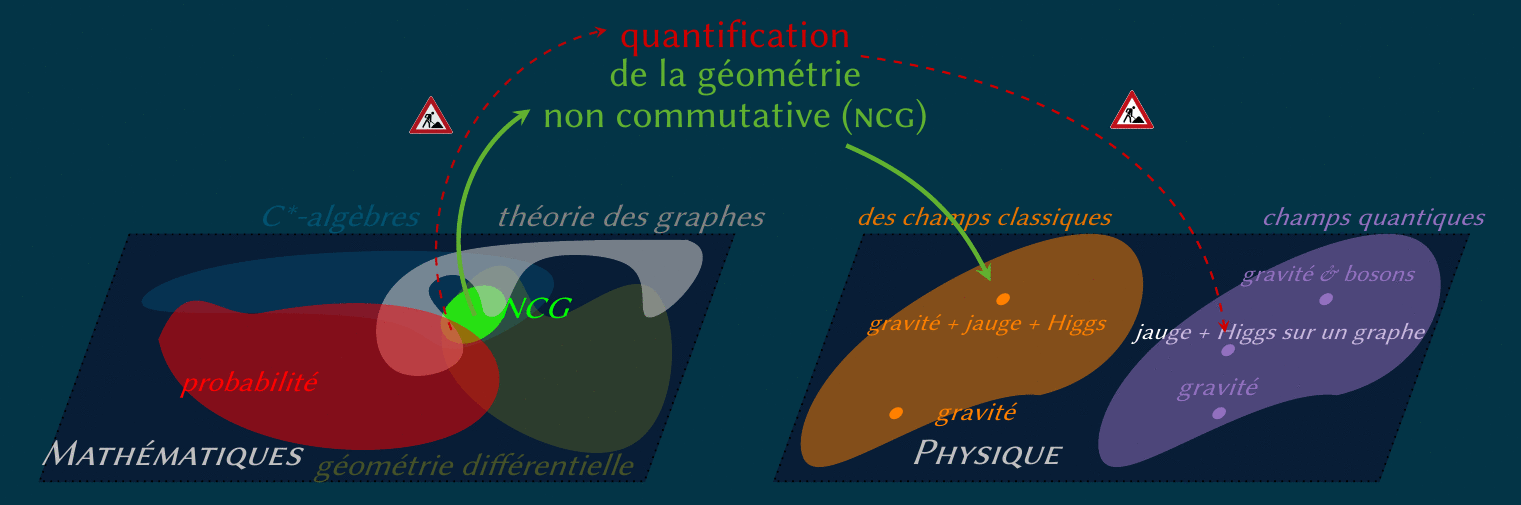
Le remplacement d'une variété par un graphe est une autre technique de discrétisation très utilisée. Comment donc faire de la théorie de jauge sur un graph générique ? Une réponse est la « décoration » des nœuds par des C*-algèbres et des arêtes par des unitarités. (Pour coller toutes ces données, des spécifications techniques sont bien sûr nécessaires.) D'un point de vue mathématique, cela signifie représenter le graph, qui est alors appelé carquois , dans une catégorie liée aux C*-algèbres.



L'espace de toutes ces représentations est caractérisé et identifié avec des triples spectraux sur le graphe. J'étudie les fonctions de partition définie par cette construction (mathematiquement avec les equations de Makeenko-Migdal et sur l'ordinateur à l'aide du « bootstrap », par example).

Il est souvent impossible, techniquement, de définir une fonction de partition sur les espaces lisses (variétés différentiables) dont on a besoin pour décrire la théorie classique de la gravité. Au moins du point de vue de la calculabilité – mais avec l'espoir d'une meilleure conception – les approximations discrètes peuvent être utiles. Par exemple, l'approximation simplicial (ou « PL-variété») des variétés lisses : Les tenseurs aléatoires (dont la limite large-N a été découverte par R. Gurău) génèrent justement de tels complexes, dont la courbure peut être calculée en utilisant le formalisme de Regge(-Einstein-Hilbert).



Une fois qu'un candidat à une théorie de la gravité quantique est formulé, il faut un outil qui permette l'interpolation entre les hautes (UV) et les basses (IR) énergies. Dans ce contexte, je me suis également intéressé récemment aux aspects mathématiques du groupe fonctionnel de renormalisation (ou équation de Wetterich).

Impressum:

Carlos Perez-Sanchez

Institut für Theoretische Physik,

Philosophenweg 19, 69120, Heidelberg, Allemagne.

téléphone: +49-6221-54-9457, et mon courrier:







I don't read French, send me back to English home page