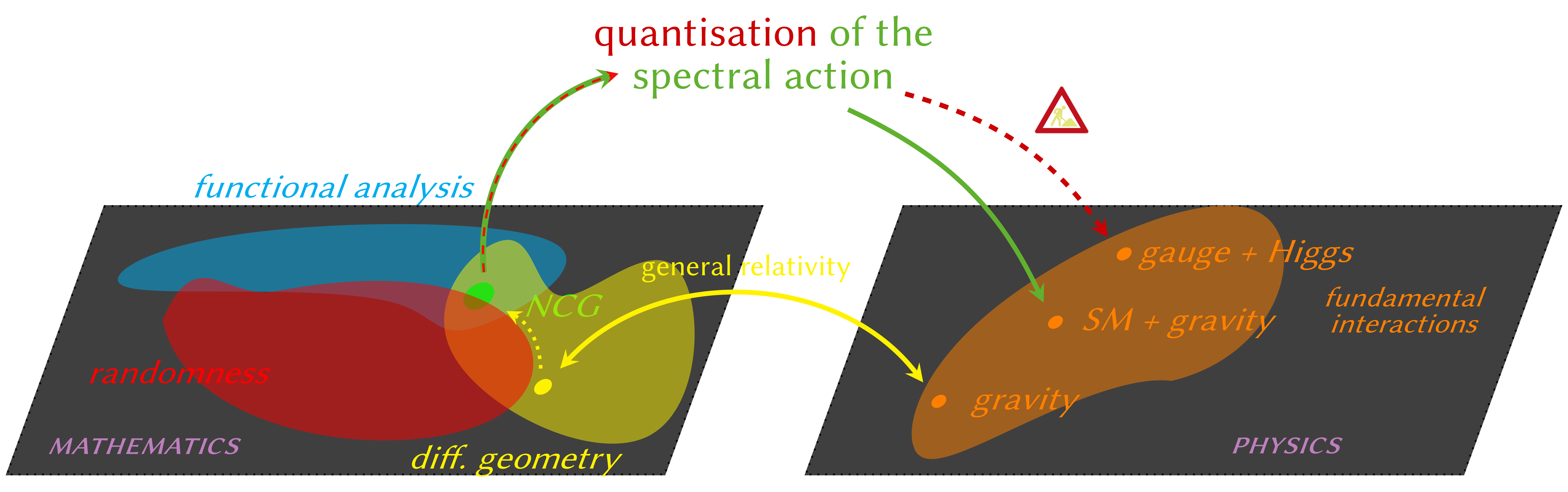
In a related but independent approach, another type of matrix ensemble emerges
when one considers
.
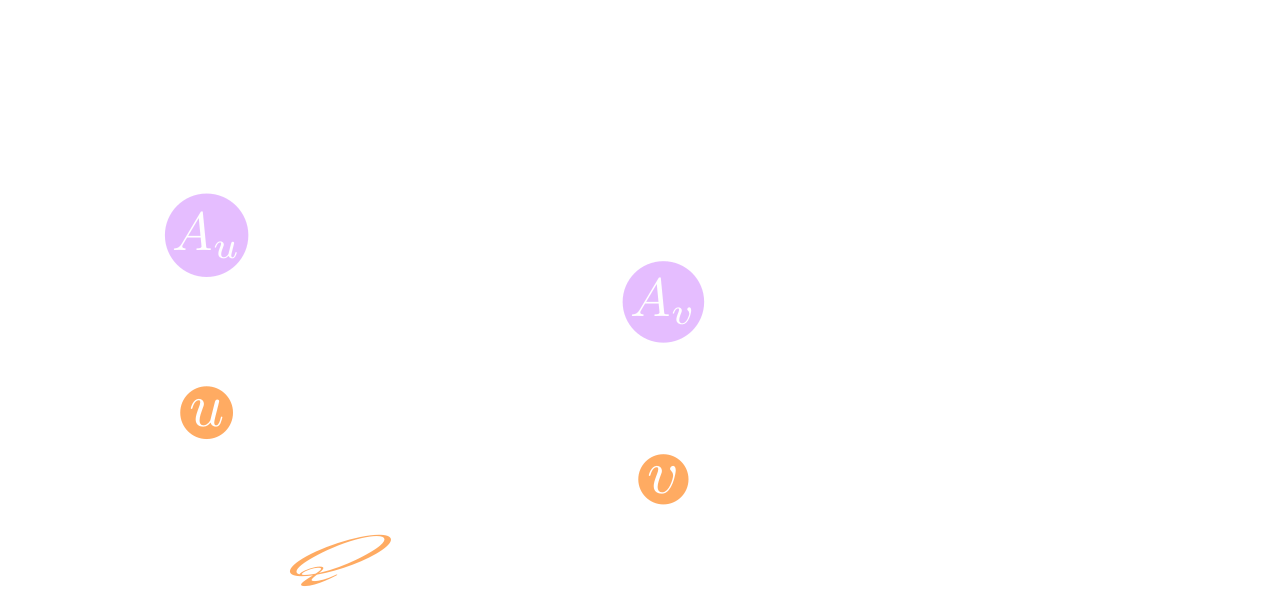
When additional data decorate the vertices (nodes) and the edges (links) of a graph one often refers to it as 'quiver'.
In our case vertices \(v\) carry
certain C*-algebras \(A_v\) and Hilbert spaces \(H_v\),
while paths \(\gamma: u\to v\) on the graph are labelled by maps \(\phi_\gamma\) between the algebras
at the endpoints \(\phi_\gamma: A_u \to A_v\),
along with unitarities \(\mathrm{hol}_\gamma: H_u\to H_v\) called holonomies, as exposed
relies on Baez' and on that of Marcolli-van Suijlekom, who first used
quivers in this context, although a different target category).
These matrix ensembles are no longer hermitian but unitary––as in lattice field theory
to which this theory reduces when it ought to.
Such unitary matrices are the ingredient to construct a Dirac operator, which together
with the pair \( \oplus_v A_v, \oplus_v H_v\) yields a
–– that is, a noncommutative geometry.
To understand its dynamics, the spectral action was computed (cf. details
) as a
certain expansion over the holonomy of loops on the graph, which generalise Wilson-plaquettes.
This way, the Dirac operator path integral
is transformed into an ensemble of unitary matrices for which

A third topic I'm interested in deals with simplicial
or (singular) PL-approximations of manifolds, which can be generated
by the Feynman expansion of tensor integrals, whose
large-
N was an essential finding by Gurău. Under precise rules (e.g.
index contraction = face identification), tensors represent simplices
and thereby Feynman graphs of invariant tensor polynomials yield simplicial gluings.
In this context, I am interested in topological and
geometric problems.

I also used quantum field theoretical techniques for
random tensors,
like
the loop (or Dyson-Schwinger) equations proven here and
this Ward-Takahashi Identity, as well as on
the geometric interpretation of their correlation functions, as sketched below.
A result with a combinatorial component is the Tutte-like recursion satisfied
by the correlation functions or moments of tensor integrals,
as proven at the end
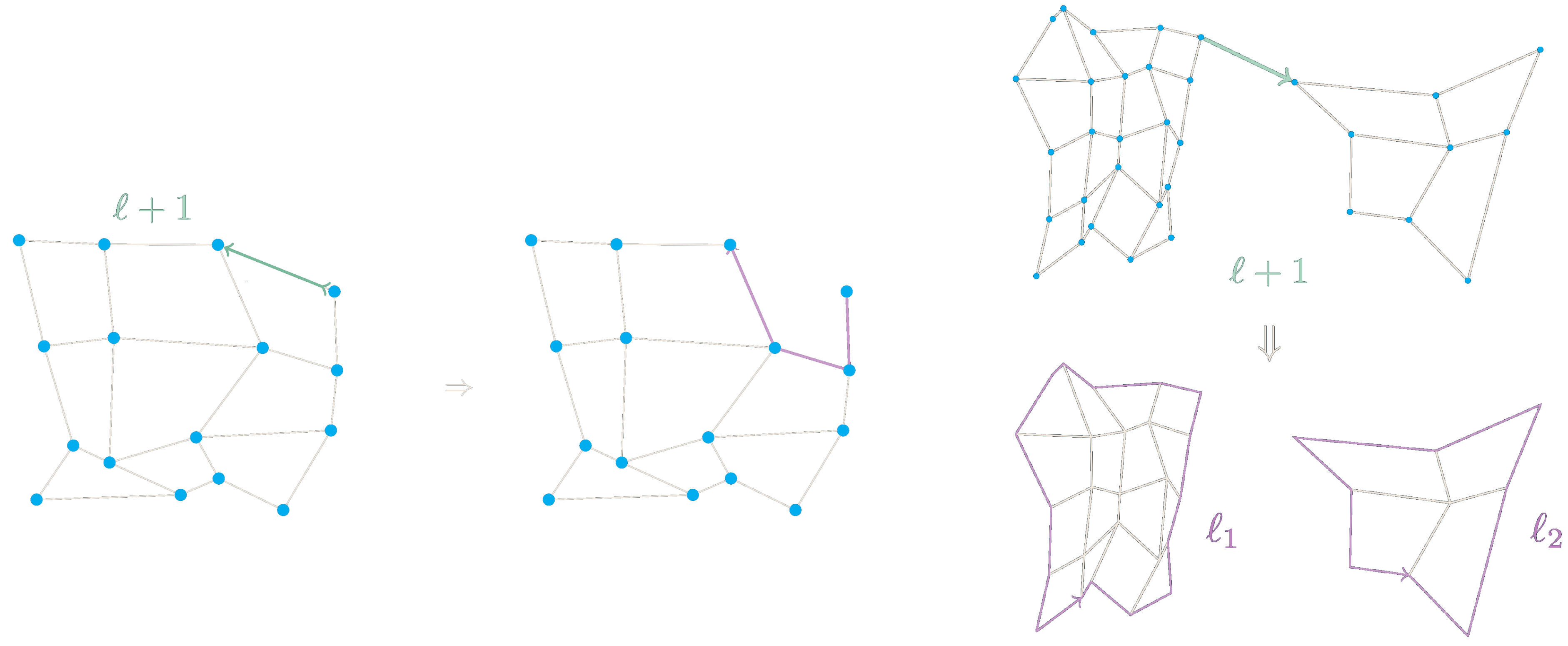
of this article. Briefly, the original recursion by Tutte is a statement in two dimensions that describes how
generating series \(\mathcal{T}_{\ell_1,\ldots,\ell_n} \) of polygonal gluings with boundaries
of prescribed perimeters \( \ell_1,\ldots, \ell_n \) are related
among themselves. This can be proven with loop equations for matrix integrals or, combinatorially deduced,
by edge-removals. In the case of the pictures below for planar rooted quadrangulations,
one has \( \mathcal{T}_{\ell+1} = \lambda \mathcal{T}_{\ell+3} +\sum_{\ell_1 + \ell_2 = \ell -1} \mathcal{T}_{\ell_1} \mathcal{T}_{\ell_2} \),
as interpreted in the picture below,
where the coefficient \( [\lambda^q]\mathcal{T}_{\ell} \)
of \( \lambda^q\) in the generating series \(\mathcal{T}_{\ell} \)
yields the number gluings with \(q\) quadrangles
with one boundary of perimeter \(\ell\).
The tensor analogue of Tutte's recursion describes
the three-dimensional situation for simplices
generated by quadratic-quartic tensor integrals.

For given boundary data \(\mathcal{D}=(\mathcal{R},\mathcal{Q})\) that can be grasped as the higher-dimensional
analogue of the perimeters in Tutte's two-dimensional case (hence \(\mathcal{R}\) and \(\mathcal{Q} \) represent
discrete closed surfaces,
since we are in one dimension higher), the obtained
equations are sketched above. These describe several generating series \( \mathfrak f_{\mathcal R},\varsigma({\mathcal D}),\ldots,\) etc.
(blobs in cyan) that yield, after contraction with the quartic tensor invariant
(depicted in form of a pillow), the initial boundary data. The proof of this claim is not combinatoric,
but uses
this tensor Ward Identity,
motivated by the work of
Dissertori-Gurău-Magnen-Rivasseau for matrix integrals, along
with
the loop equations. (This combination
was a key strategy for
the
Grosse-Wulkenhaar model.)

Working with
functional renormalisation, particularly with Wetterich equation,
I focused first
(
in this article)
on matrix models motivated by noncommutative geometry
as mentioned above. The parameter of the RG-flow is
(the logarithm of) a threshold on the Dirac spectrum,
which in the two-sphere is related to the azimuthal
number \(\ell\) and can be depicted as:
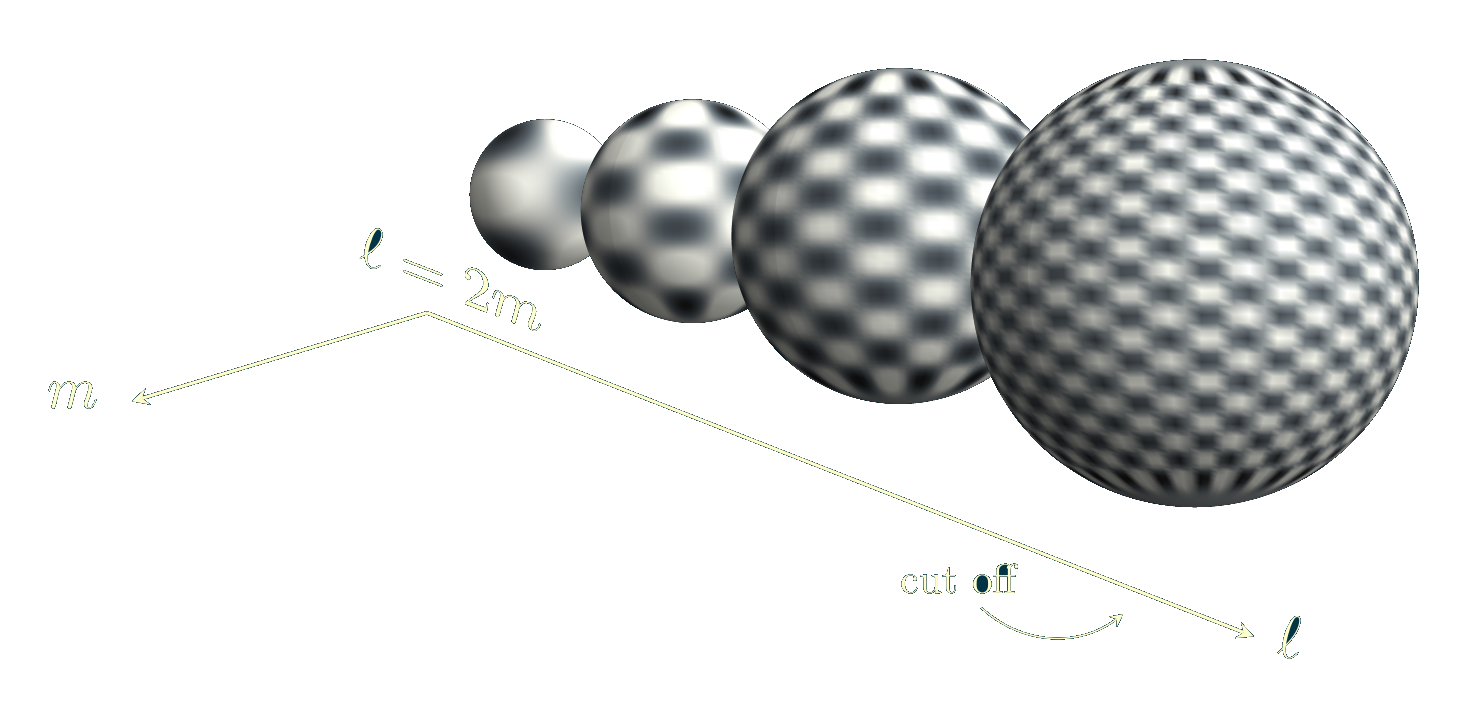
The interactions (or equivalently, the probability measure)
governing these models contain certain products of traces of polynomials in several matrices
like \(\mathrm{Tr}(A^2) \times \mathrm{Tr}(B^2) \) or \(\mathrm{Tr} (A BC+CBA).\)
The Wetterich equation in functional renormalisation traces powers of the Hessian
of such expressions and, particularly due to the double traces,
obeys an algebra I found interesting
and described here.
Indeed, using (a bigger 'cousin' of) the free algebra speeds up computations and has a transparent Feynman diagrammatics interpretation.
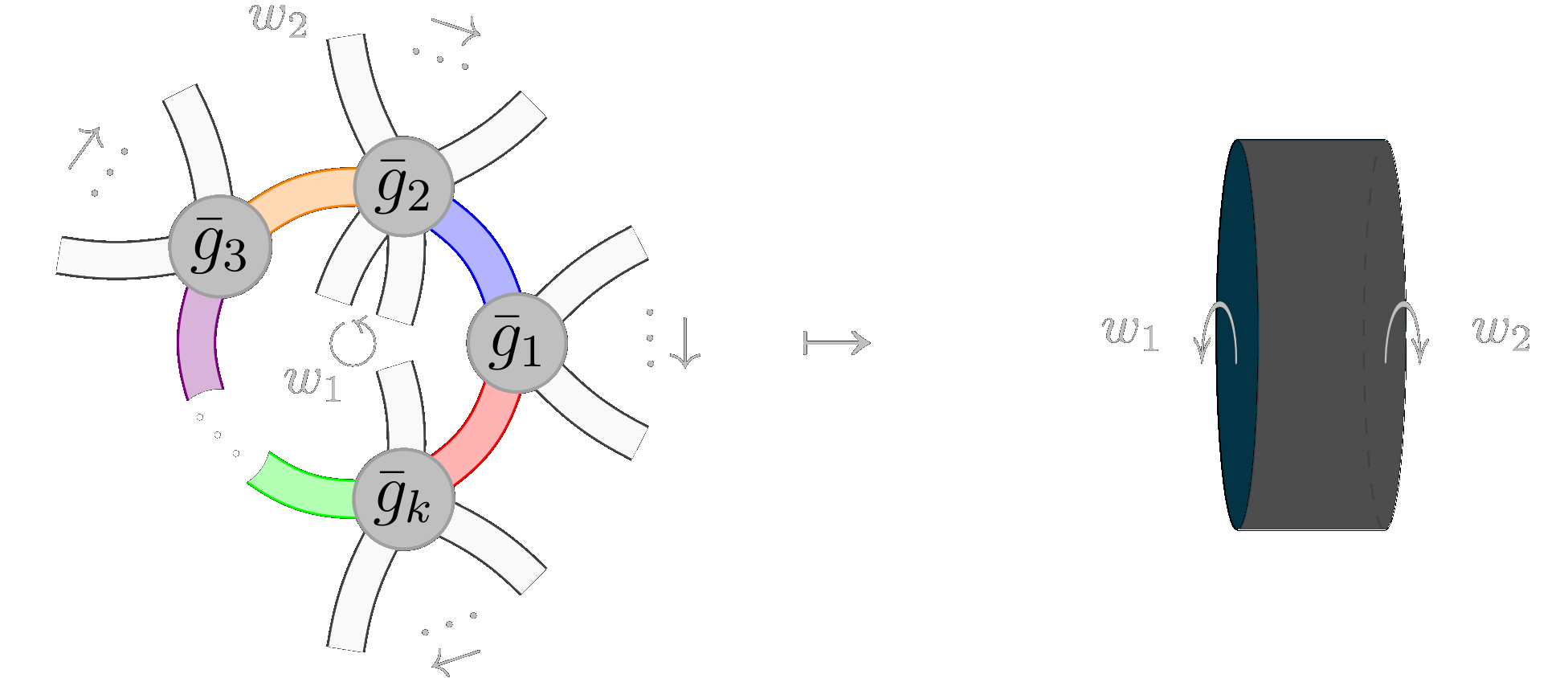
The need for an algebraic structure, as opposed to graph combinatorics or to a matrix entries computation,
can be motivated by the next ribbon-graphical example, where white-filled strands represent a matrix,
while those in solid colour a derived matrix.

(Definitions for \( \boxtimes \) and \(\otimes \),
to wit how this algebra works, are explained
here.) These latter strands in solid colour form a loop when Hessians are multiplied and traced, and the uncontracted white-filled edges––read
off in the proper order the words \( w_1\) and \( w_2\) around the two boundaries of that loop––yield the effective interactions, e.g. \(\mathrm{Tr} (w_1) \times \mathrm{Tr}(w_2)\) in the case below
that illustrates a generic model:

Lately I'm interested in the
bootstrap approach to random tensors and random matrix integrals.
Bootstrap usually evokes a conformal field theory context, but in the present case it
just means to exploit the (easy to prove, albeit powerful) fact that a certain
matrix of expectation values, typically Hankel- or Toeplitz-shaped, is positive.
As the size of its upper-left block submatrices grows, one gets tighter and tighter constraints
from the sign of their determinant, which
eventually yield the solution to the model (in the sense that a family of
expectation values is determined in terms of the coupling and thus, by loop equations, the
whole correlation functions).
Applying the bootstrap to the simplest interesting quiver
(details
here),
whose partition function boils down to the Gross-Witten-Wadia integral, yields
the following. The planes represent the coupling \(x\) and the first moment
\(y\), and specifically, the red region denotes the negativity of the determinant of
said \(2\times 2\) submatrix, the orange one that of the \(3\times 3,\ldots, \)
the blue region of the \(6\times 6\)
block, etc. Hence the solution \(y(x)\) must lie in all the transparent
regions
simultaneously.
The exact solution in the rightmost plot
shows neat agreement with the bootstrap:


Without having published on the next topics, I'm also interested in JT-gravity
(
short handout from our STRUCTURES-seminar), Topological Recursion
(
handout from a talk)
and lately in free probability, the BV-formalism and Weingarten calculus.
I work in the group of
Răzvan Gurău
at the Institute of Theoretical Physics, University of Heidelberg. Before, I was a postdoc in the group of
Piotr Sułkowski at the
Institute of Theoretical Physics, University of Warsaw, Poland. Prior to that,
I did my Ph.D. in mathematics at the University of Münster, under supervision of
Raimar Wulkenhaar.
This term I am teaching Theoretical Statistical Physics in the MSc programme (
Tutorium WiSe 24/25).
Thanks for visiting!
Kontakt:
Carlos Perez-Sanchez
Philosophenweg 19
69120, Heidelberg, Deutschland.
Tel. +49-6221-54-9103
My e-mail is:

 Deutsch
Deutsch  Español
Español  Français
Français  Polski
Polski 


![[Sorry. Maybe in other browser you could see an animation of the
Harer-Zagier function for d=3]](arXiv2401.03705HarerZagierd=3oeisorgA005899.gif)